My interests..
..are primarily focused on the exploration of ultracold quantum gases with numerical techniques. In particular, I am interested in systems that feature some sort of imbalance such as mass and/or spin asymmetry. To this end, I use and develop Monte Carlo methods in a variety of flavors.
This is a short overview on some of my recent projects - for the full experience you can find my work on arXiv.
Revealing pairing patterns with the shot noise
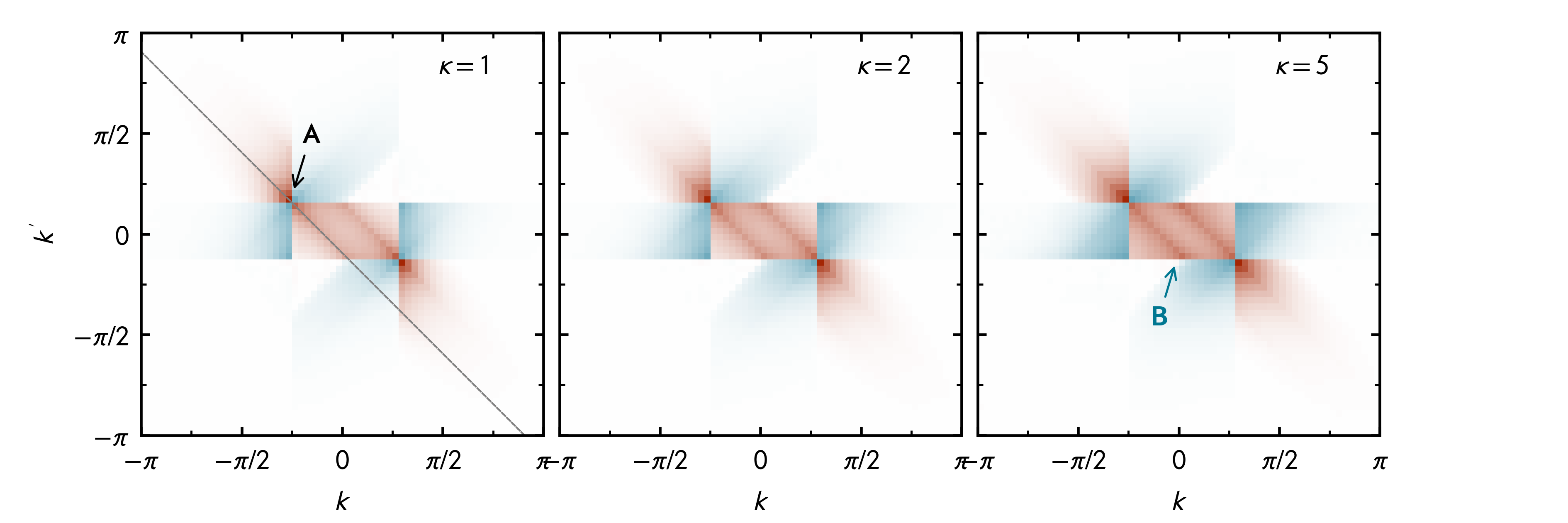At the heart of our favorite quantum effects - superfluidity and superconductivity - is the formation of electron pairs. Usually, with an equal amount of spin-up and -down particles present, these Cooper pairs form such that their total momentum vanishes. With a spin-imbalance, on the other hand, the pairs pick up a finite center-of-mass momentum. An exeptionally clean probe to study such phenomena is given by the correlation of fluctuations, also called shot-noise. Interestingly, in addition to the leading peak that is expected for 1D fermions, we also found a subleading contribution at the same total momentum but at different areas in momentum space - a novel pairing mechanism that emerges with inceasing mass-imbalance. What's exciting about this is that the shot-noise is directly available from time-of-flight images in experiments - so this theoretical prediction is of direct experimental relevance!
Unitary fermions & spin imbalance
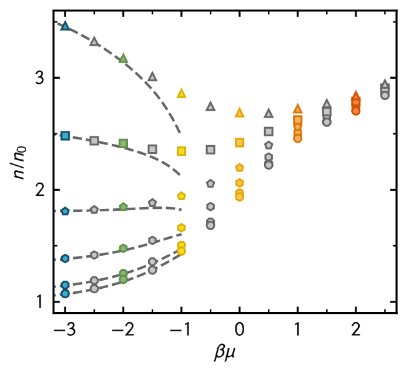One of the most remarkable features in cold atom experiments is the ability to tune the interaction strength between particles. For Fermi systems, this allows
us to study the crossover from weakly interacting fermions to tightly bound fermionic molecules. Right in the "middle" of this so-called BCS-BEC crossover,
in a regime where the scattering length dominates all other length scales, sits the unitary Fermi gas (UFG).
One observes universal behavior in the sense that thermodynamic properties cease to depend on the exact microscopic interaction
for sufficently short-ranged inter-particle potentials. In a recent project we used the CL method to study the UFG in the presence of a finite population imbalance.
In our work we predict the density-equations of state over a wide range of spin-asymmetries and temperatures above the superfluid regime. These EOS can be used
to infer knowledge on the phase diagram, which still lacks ab-initio treatment at finite spin imbalance.
Fermi mixtures: mass imbalance
Many recent quantum gas experiments involve mixtures of two atomic species. For two fermionic species an unequal mass could lead
to interesting consequences such as inhomogeneous pairing at low temperature. Theoretically, however, these systems are challenging to treat due to the reduced symmetry.
Within this project, we investigated the applicability of two comsasdputational methods (iHMC & CL) to study mass-imbalanced systems by performing a case study for 1D fermions.
We observe excellent agreement among the methods and obtain ground-state equations of state as a function of the coupling.
Complex Langevin (CL)
Whenever we want to study fermionic many-body systems with Monte Carlo methods we face a major road-block: the sign-problem. It causes the algorithms to scale exponentially with increasing system size and so we quickly run out of steam even on the largest available HPC clusters.
Recent progress in the area of high-energy physics inspired us to adapt the so-called complex Langevin method to ultracold quantum systems as a way to circumvent this nasty problem. The method itself is known since the mid 80s and has had mixed success due to some mathematical shortcomings for certain theories. However, it turns out that it is a valuable tool in the study of ultracold Fermi gases, as we have shown for a variety of imbalanced systems.
From few to many with Hybrid Monte Carlo (HMC)
It turns out, that the answer to the question "How many is many?" poses a formidable challenge and is highly dependent on the spatial dimension. Nevertheless, an answer is needed to know when we can reliably use effective many-body descriptions to infer macroscopic propierties of the system under study. While there are certain exact solutions available in one dimension, these work best in the thermodynamic limit and exact numbers for finite systems are often challenging to come by. In larger spatial dimensions, exact solutions are entirely unkown and thus numerical studies are our only way to address these questions.
